[This post was first published on Medium].

This is part III in a series of posts (which was not intended to be a series) on the consequences of Bitcoin’s declining block rewards to the security of the network.

Part I: Bitcoin Security: a Negative Exponential. Tweetstorm.

Part II: Bitcoin Security in One Chart. Tweetstorm.

In the first post I argued that the attack cost (and therefore security) of proof-of-work systems like Bitcoin is ultimately determined by miner revenue — the “security budget”.

To illustrate this relationship I used a simplified model-cryptocurrency with constant miner pay-out and no ASICs. I did include a second, shorter example with ASICs, but I didn’t spend much time on it.

It seemed to me that ASICs change the attack cost profile (by “front-loading” attack cost) but that security budget still dominates the attack cost equation — which is all that mattered for my argument.

But, to close out the trilogy I felt I needed to go down this avenue and find out for sure whether attack cost is ultimately determined by security budget — ASICs or no ASICs!

Initial Hardware

So you want to 51% attack Bitcoin (or any ASIC-mined PoW system). First you need to buy the hardware. How much will that cost?

Suppose the network is producing 10TH/s. Worst-case scenario you must also buy 10TH/s worth of hardware, then you have 50% of total hash power. In reality less efficient miners will drop-out as you add hash power and kill their margins, so in the best-case you could buy as little as ~5TH/s.

But we care about cost, not absolute hash power. How do miners decide how much capital should be tied-up in ASICs at any given time?

Present Value of Income Stream

Miners are funded by the income stream that the protocol provides (block rewards + tx fees). They care about the dollar amount of this stream. This is the security budget that I talked about in the previous posts.

The magnitude ($/time) of this stream is determined by coin price, inflation rate, and block space demand. Miners have no impact on the income stream unless they affect the factors mentioned — they simply split the income stream (whatever it is) based on their respective hash power contribution.

Miners buy ASICs in order to capture some sliver of the income stream. If they are rational they do not spend more on hardware than the present value of the expected income stream sliver (costs deducted) that they plan to capture with the hardware.

Note: These income streams and cost streams are projections into the future. Expected profit from these streams must be heavily discounted to account for various risk-factors and uncertainties (see appendix).

Present Value Equation

The present value of some income stream can be determined with the… present value equation:

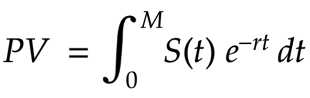
Variables: PV is the present value of the income stream. S(t) is the income stream. The limits of integration, O and M, define the time-span, and r is the going interest rate (5% or whatever).

The equation tells how much money you would need now, such that by the end of some period, you were just as well-off as someone who had the income stream — it really does give the present value of the income stream.

Applying this equation to the miner situation we get:

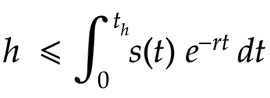
Variables: h is how much the miner spends on hardware. The upper limit of integration, th is the profitable life-span of the hardware. s(t) is the expected income stream. r is the usual interest rate.

The income stream that the miner cares about in this calculation is actually the income stream after expenses. If p(t) is the expected operational cost (electricity, rent, etc) then we get:

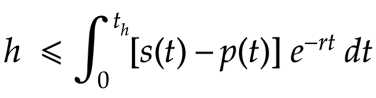
So, miners buy a unit of hardware if they think that the present value of the expected, risk-discounted, income stream that the unit will capture — minus the costs to run it — exceeds the cost of the hardware.

Summed Across all Miners

Each miner does this calculation individually — they claim a fraction of the overall income stream (security budget) by spending less than the present value of the stream fraction.

When you sum this behaviour across all miners you sum all fractions of the larger income stream, and you sum the respective hardware-spends for each fraction.

The result of this summation is that the miners collectively spend on hardware less than the risk-adjusted present value of the total expected income stream — the security budget!

How could it be otherwise? If the miner-collective were consistently* spending more capturing the income stream than the present value of the income stream they would effectively be losing money — which can’t last.

But, suppose miners overestimate the income stream and spend more on hardware than they should, what is the value of this hardware?

The value of the hardware at any point in time is defined as the present value of the income stream captured by the hardware! Regardless of what the miners paid for the hardware, it is now worth exactly the present value of whatever income it’s expected to capture.

If you wanted to buy some of that hardware from the miners you would not pay what they paid for it. You would not pay a penny more than PV of what it is going to earn for you. Likewise, ASIC sellers will not be able to sell hardware for more than PV of what they are expected to capture…

So the total hardware value** for the whole network, H is capped by the projected security budget, S(t) minus operational cost P(t). tH is the average hardware lifespan:

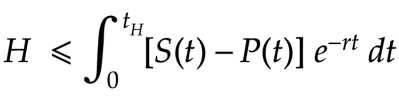
* Hardware spend is based on a projection of the future. If the projection is wrong miners can over-spend or under-spend on hardware. This uncertainty is factored into spend however, and will tend to smooth out over time. See appendix.

** Assuming hardware is upgraded continuously the average unit will be middle-aged, so tH may be too wide — overestimating cost. On the other hand newer units may represent majority hash power, and it’s possible a new hardware release just occurred and most units are very young.

What if ASICs Stop Advancing

If ASIC advancement plateaus then miners only need to buy hardware once, then can mine forever. tH is then infinite. Does H get huge? Does this break the bound?

No. When tH is infinite the expression converges:

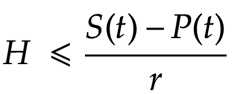
Operational & Upgrade Costs

So we’ve got a cap on the hardware cost.

Now we need to consider the cost of running all that hardware, and the cost of upgrading the hardware throughout the attack*.

I think I found an exact description of total upgrade cost (see appendix), but couldn’t find the math to express it. Instead I’m using S*(t) — the actual total miner revenue paid out over time (the previous S was projected revenue) — as a rough bound on upgrade cost and operational cost (electricity etc).

Miners won’t spend more money running their hardware than they earn. They could spend a lot on hardware though. So, for short time frames total expenditure could exceed total revenue, but this will become smoothed out over time — taking at most one hardware refresh period — revenue must exceed expenditures for long time frames.

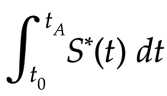
Variables: S*(t) is actual total revenue. t0 is when the attack starts, tA is when the attack ends.

But if the attacker has half the hash power, don’t they get half the revenue — half of S*(t)? If so, honest miners would have half of S*(t) to spend on operations and upgrades. Then the attacker could match their spend with his “attack-income”. Then this whole term would become zero.

I’m not sure how this would actually play out, but I don’t think this income can be counted on, and it doesn’t matter for my argument. So, I’ll assume the attacker gets no income and use the safe upper bound of S*(t).

* It seems unlikely that miners would upgrade hardware while being attacked — difficulty is now much higher, and long-term confidence is low — but I’m assuming worst case for the attacker.

Final Expression

Combining the initial hardware investment cost (the first integral) with the operational and upgrade cost (second integral) we get:

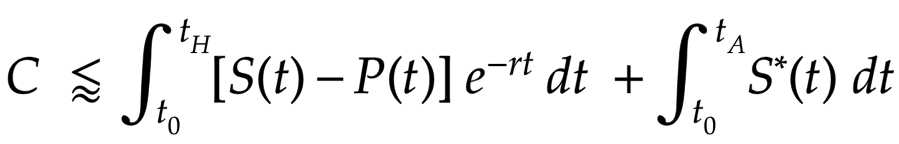
Conclusion

So the equation has S, S*, P, r, and the bounds t0, tH, tA:

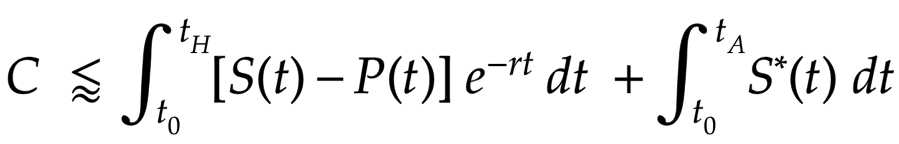
The interest rate r is external to the protocol so that can be treated as a constant. tA, and t0 are free-variables of sorts. tH is determined by external things like R&D pace and is outside the realm of the protocol.

So, that just leaves S, S* and P. It doesn’t really matter what P does — it’s capped by S, and cost is highest when it’s small anyway. S and S* are just different forms of the security budget — one is a projection, the other is actual. So it all comes down to the security budget.

Security budget dominates attack cost — ASICs or not!

---

Part I: Bitcoin Security: a Negative Exponential.

Part II: Bitcoin Security in One Chart.

Thanks to Dino Arturo Celotti, Chris McCoy, Matteo Leibowitz, and Jason Varner.

Appendix

More Precise Description of Upgrade Cost

The network upgrades in discrete chunks. A miner does a calculation and determines they can capture some slice of the overall income stream, S(t) for less than PV of that stream slice.

Miner 1 finds PV for their expected slice of the current projection of S(t), and spends less than that amount on hardware. Miner 2 finds PV for their expected slice of a new projection of S(t) and spends less than that on hardware. And so on. S(t) is a projection — it is updated for each iteration.

So the total amount spent on hardware for the network for some period should be capped by the sum of all the PV’s of these slices of changing S(t) streams calculated by upgrading miners, for this period.

This could be expressed as a sum of integrals, but we don’t know how many discrete upgrades happen — it seems it should be a double integral of some sort. I tried this but didn’t get it worked out.

Discounting Income Streams

Assuming hardware advances, the total hash power produced by a network will tend to increase even if security budget (total miner revenue) is constant. So the percentage of total hash power produced by any given piece of hardware will decline over time.

Therefore s(t), the income stream captured by any piece of hardware, is downward sloping.

At some point the hardware costs more to run than it’s worth, so the revenue stream, s(t)-p(t) goes to zero. This happens after a period of time tH.

The overall income stream also tends to decline (declining block rewards). This must be factored into miners long term decisions.

The income stream, s(t) must also be heavily discounted due to risk — it depends on price, block rewards and fees, two of which are unpredictable.

All these factors and uncertainties result in miners heavily discounting the expected value of their income stream.

Hardware Over-Allocation Smooth Out

Hardware spend is based on the present value (PV) of a projection of some income stream. If things are booming the projected income stream might justify the miners buying lots of hardware.

Then a downturn happens, projected income is low, and miners have “too much” hardware. However they keep mining as long as they aren’t losing money.

Miners of course try to avoid this by being conservative with their hardware purchases, and generally preferring to upgrade as rarely as they can. Over-allocations should also smooth out over time. Miners who consistently over-allocate on hardware will get bled out.

---